Springboard Logistic Regression Advanced Case Study¶
$$ \renewcommand{\like}{{\cal L}} \renewcommand{\loglike}{{\ell}} \renewcommand{\err}{{\cal E}} \renewcommand{\dat}{{\cal D}} \renewcommand{\hyp}{{\cal H}} \renewcommand{\Ex}[2]{E_{#1}[#2]} \renewcommand{\x}{{\mathbf x}} \renewcommand{\v}[1]{{\mathbf #1}} $$This case study delves into the math behind logistic regression in a Python environment. We've adapted this case study from Lab 5 in the CS109 course. Please feel free to check out the original lab, both for more exercises, as well as solutions.
We turn our attention to classification. Classification tries to predict, which of a small set of classes, an observation belongs to. Mathematically, the aim is to find $y$, a label based on knowing a feature vector $\x$. For instance, consider predicting gender from seeing a person's face, something we do fairly well as humans. To have a machine do this well, we would typically feed the machine a bunch of images of people which have been labelled "male" or "female" (the training set), and have it learn the gender of the person in the image from the labels and the features used to determine gender. Then, given a new photo, the trained algorithm returns us the gender of the person in the photo.
There are different ways of making classifications. One idea is shown schematically in the image below, where we find a line that divides "things" of two different types in a 2-dimensional feature space. The classification show in the figure below is an example of a maximum-margin classifier where construct a decision boundary that is far as possible away from both classes of points. The fact that a line can be drawn to separate the two classes makes the problem linearly separable. Support Vector Machines (SVM) are an example of a maximum-margin classifier.

%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import pandas as pd
pd.set_option('display.width', 5000)
pd.set_option('display.max_columns', 100)
pd.set_option('display.notebook_repr_html', True)
import seaborn as sns
sns.set_style("whitegrid")
sns.set_context("poster")
from PIL import Image
import sklearn.model_selection
c0=sns.color_palette()[0]
c1=sns.color_palette()[1]
c2=sns.color_palette()[2]
from matplotlib.colors import ListedColormap
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
def points_plot(ax, Xtr, Xte, ytr, yte, clf, mesh=True, colorscale=cmap_light,
cdiscrete=cmap_bold, alpha=0.1, psize=10, zfunc=False, predicted=False):
h = .02
X=np.concatenate((Xtr, Xte))
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
#Return coordinate matrices from coordinate vectors
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
#plt.figure(figsize=(10,6))
if zfunc:
p0 = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 0]
p1 = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z=zfunc(p0, p1)
else:
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
ZZ = Z.reshape(xx.shape)
if mesh:
plt.pcolormesh(xx, yy, ZZ, cmap=cmap_light, alpha=alpha, axes=ax,
shading='auto')
if predicted:
showtr = clf.predict(Xtr)
showte = clf.predict(Xte)
else:
showtr = ytr
showte = yte
ax.scatter(Xtr[:, 0], Xtr[:, 1], c=showtr-1, cmap=cmap_bold,
s=psize, alpha=alpha, edgecolor="k")
# and testing points
ax.scatter(Xte[:, 0], Xte[:, 1], c=showte-1, cmap=cmap_bold,
s=psize+10, alpha=alpha, marker="s")
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
return ax,xx,yy
def points_plot_prob(ax, Xtr, Xte, ytr, yte, clf, colorscale=cmap_light,
cdiscrete=cmap_bold, ccolor=cm, psize=10, alpha=0.1):
ax,xx,yy = points_plot(ax, Xtr, Xte, ytr, yte, clf, mesh=False,
colorscale=colorscale, cdiscrete=cdiscrete,
psize=psize, alpha=alpha, predicted=True)
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=ccolor, alpha=.2,
# axes=ax
)
cs2 = plt.contour(xx, yy, Z, cmap=ccolor, alpha=.6,
# axes=ax
)
plt.clabel(cs2, fmt = '%2.1f', colors = 'k', fontsize=14,
# axes=ax
)
return ax
A Motivating Example Using sklearn: Heights and Weights¶
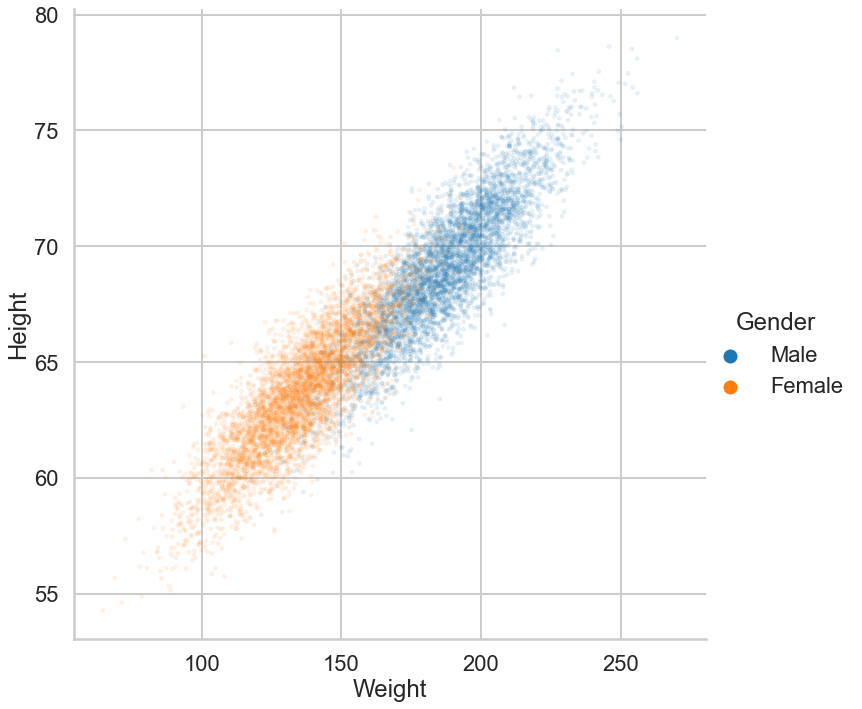
We'll use a dataset of heights and weights of males and females to hone our understanding of classifiers. We load the data into a dataframe and plot it.
dflog = pd.read_csv("data/01_heights_weights_genders.csv")
dflog.head()
Remember that the form of data we will use always is

with the "response" or "label" $y$ as a plain array of 0s and 1s for binary classification. Sometimes we will also see -1 and +1 instead. There are also multiclass classifiers that can assign an observation to one of $K > 2$ classes and the labe may then be an integer, but we will not be discussing those here.
y = [1,1,0,0,0,1,0,1,0....].
Checkup Exercise Set I
- Exercise: Create a scatter plot of Weight vs. Height
- Exercise: Color the points differently by Gender
# your turn
# sns.jointplot(data=dflog,x='Weight',y='Height',hue='Gender',alpha=0.1,edgecolor = None,s=17,height=10)
sns.relplot(data=dflog,x='Weight',y='Height',hue='Gender',alpha=0.1,edgecolor = None,s=17,height=10)
Training and Test Datasets¶
When fitting models, we would like to ensure two things:
- We have found the best model (in terms of model parameters).
- The model is highly likely to generalize i.e. perform well on unseen data.
Purpose of splitting data into Training/testing sets
- We built our model with the requirement that the model fit the data well.
- As a side-effect, the model will fit THIS dataset well. What about new data?
- We wanted the model for predictions, right?
- One simple solution, leave out some data (for testing) and train the model on the rest
- This also leads directly to the idea of cross-validation, next section.
First, we try a basic Logistic Regression:
- Split the data into a training and test (hold-out) set
- Train on the training set, and test for accuracy on the testing set
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score,classification_report,confusion_matrix
# Split the data into a training and test set.
Xlr, Xtestlr, ylr, ytestlr = train_test_split(dflog[['Height','Weight']].values,
(dflog.Gender == "Male").values,random_state=5)
clf = LogisticRegression()
# Fit the model on the trainng data.
clf.fit(Xlr, ylr)
predictions = clf.predict(Xtestlr)
# Print the accuracy from the testing data.
print(accuracy_score(predictions, ytestlr))
print(confusion_matrix(ytestlr,predictions))
print(classification_report(ytestlr,predictions))
Tuning the Model¶
The model has some hyperparameters we can tune for hopefully better performance. For tuning the parameters of your model, you will use a mix of cross-validation and grid search. In Logistic Regression, the most important parameter to tune is the regularization parameter C. Note that the regularization parameter is not always part of the logistic regression model.
The regularization parameter is used to control for unlikely high regression coefficients, and in other cases can be used when data is sparse, as a method of feature selection.
You will now implement some code to perform model tuning and selecting the regularization parameter $C$.
We use the following cv_score function to perform K-fold cross-validation and apply a scoring function to each test fold. In this incarnation, we use accuracy score as the default scoring function.
- K-fold cross-validation
- test fold
- incarnation
?? Where is incarnation?
In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
nfold = 5
def cv_score(clf, x, y, score_func=accuracy_score):
result = 0
# nfold = 5
# split data into train/test groups, 5 times
for train, test in KFold(nfold,
# shuffle=True,
# random_state=50,
).split(x):
# fit
clf.fit(x[train], y[train])
print(f'\tscore_func = {score_func(clf.predict(x[test]), y[test])}')
# evaluate score function on held-out data
result += score_func(clf.predict(x[test]), y[test])
# average
return result / nfold
=========note===============
.accuracy_score() Accuracy classification score.
============================
Below is an example of using the cv_score function for a basic logistic regression model without regularization.
# example of using the `cv_score` function
print('=== An example of Manual CV ===')
clf = LogisticRegression()
score = cv_score(clf, Xlr, ylr)
print(f'The ave rage score is {score} with default C(=1.0) and nfold = {nfold}')
Checkup Exercise Set II
Exercise: Implement the following search procedure to find a good model- You are given a list of possible values of `C` below
- For each C:
- Create a logistic regression model with that value of C
- Find the average score for this model using the `cv_score` function **only on the training set** `(Xlr, ylr)`
- Pick the C with the highest average score
#the grid of parameters to search over
Cs = [0.0001,0.001, 0.1, 1, 10, 100]
# your turn
from sklearn.linear_model import LogisticRegression
max_score = 0
print('=== Manual CV ===')
for c in Cs:
clf = LogisticRegression(C=c)
score = cv_score(clf, Xlr, ylr)
print(clf,score,'\n')
if score > max_score:
max_score = score
best_C =c
(comment) The average score is same as default C (1.0)...
Checkup Exercise Set III
**Exercise:** Now you want to estimate how this model will predict on unseen data in the following way:- Use the C you obtained from the procedure earlier and train a Logistic Regression on the training data
- Calculate the accuracy on the test data
You may notice that this particular value of `C` may or may not do as well as simply running the default model on a random train-test split.
- Do you think that's a problem?
- Why do we need to do this whole cross-validation and grid search stuff anyway?
# your turn
print('=== Manual CV result ===')
Cs = [0.0001,0.001, 0.1, 1, 10, 100]
for c in Cs:
clf = LogisticRegression(C=c)
score = cv_score(clf, Xlr, ylr)
print(clf,score,'\n')
if score > max_score:
max_score = score
best_C =c
print(f'The best C was {best_C} with nfold = {nfold} \n')
clf = LogisticRegression(C=best_C)
clf.fit(Xlr, ylr)
predictions = clf.predict(Xtestlr)
print('nfold is\t',nfold)
print('Best C =\t',best_C)
print('Train accuracy:\t',max_score)
print('Test accuracy:\t',accuracy_score(predictions, ytestlr))
print('\nConfusion matrix\n',confusion_matrix(ytestlr,predictions))
print('\n',classification_report(ytestlr,predictions))
Do you think that's a problem?
Overfitting will be one of the problems.
What is observered is that the higher regularization strength(C = 0.0001,0.001), the lower score. This is because higher regularization induces more underfitting.
On the other hand, the score with C = (0.1,1,10,100,1000) does not go above and has the constant of 0.9172.
One of the reasons why this happens would be that the lower regularization(low penalty), which leads to more overfitting tendency. Although this overfitting model probably incurs zero loss in given data set, this also may have high vias and judge the future input-data incorrectly.
Assuming above discussions be true, C=0.1 is the best tradeoff between underfitting and overfitting.
Why do we need to do this whole cross-validation and grid search stuff anyway?
One of such senarios will be when the amount of data set available to set model is very small.
## Note¶
[def] cross-validation (AKA. k-Fold Cross-Validation) ==
A resampling procedure. Here, we used KFold function (from sklearn.model_selection) in cs_score. This is necessary in order to...
- avoid overfitting by repeating the same samples
evaluate machine learning models on a limited data sample
When evaluating different settings (“hyperparameters”) for estimators, such as the C, there is still a risk of overfitting on the test set. To solve this problem, more sets of training data are necessary.
However, by partitioning the available data into three sets, we drastically reduce the number of samples.
A solution to this problem is a procedure called cross-validation (CV for short). Here, we used k-fold CV (& k=5), the training set is split into k (=5) smaller sets. The following procedure is followed for each of the k “folds”:
- A model is trained using of the folds as training data;
- the resulting model is validated on the remaining part of the data (i.e., it is used as a test set to compute a performance measure such as accuracy).
This approach can be computationally expensive, but does not waste too much data (as is the case when fixing an arbitrary validation set), which is a major advantage in problems such as inverse inference where the number of samples is very small.
[def] C ==
Inverse of regularization strength; must be a positive float. Like in support vector machines, smaller values specify stronger regularization. This prevents features from having terribly high weights, thus implementing a form of feature selection.
[def] [Regularization] (https://en.wikipedia.org/wiki/Regularization_%28mathematics%29#Regularization_in_statistics_and_machine_learning)==
from stackflow A penalty to increasing the magnitude of parameter values in order to reduce overfitting. Most often the function is λΣθj2, which is some constant λ times the sum of the squared parameter values θj2. The larger λ is the less likely it is that the parameters will be increased in magnitude simply to adjust for small perturbations in the data. In your case however, rather than specifying λ, you specify C=1/λ.
[def] Loss function==
loss functions for classification are computationally feasible loss functions representing the (shape of) price paid for inaccuracy of predictions in classification problems
#¶
Black Box Grid Search in sklearn¶
Scikit-learn, as with many other Python packages, provides utilities to perform common operations so you do not have to do it manually. It is important to understand the mechanics of each operation, but at a certain point, you will want to use the utility instead to save time...
Checkup Exercise Set IV
Exercise: Use scikit-learn's [GridSearchCV](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html) tool to perform cross validation and grid search. * Instead of writing your own loops above to iterate over the model parameters, can you use GridSearchCV to find the best model over the training set? * Does it give you the same best value of `C`? * How does this model you've obtained perform on the test set?# your turn
from sklearn.model_selection import GridSearchCV
print('=== GridSearchCV result ===')
fitmodel = GridSearchCV(LogisticRegression(), param_grid={'C':Cs}, cv=5,scoring="accuracy",
# refit=False,
verbose=3)
fitmodel.fit(Xlr, ylr)
print('cv is\t',fitmodel.cv)
print('Best C =\t',fitmodel.best_params_)
print('Train accuracy:\t',fitmodel.best_score_)
print('Test accuracy:\t',accuracy_score(clf.predict(Xtestlr), ytestlr))
Instead of writing your own loops above to iterate over the model parameters, can you use GridSearchCV to find the best model over the training set?
Yes, pretty much.
Does it give you the same best value of
C?No, it doesn't.
The result of manual method(former one) and GridSearchCV is as follows.
- Best C: differnt: 0.1 > 1 (??Can we say 0.1 is better than 1 as C=1 had more pushment leading to more overhitting than the other?)
- Train accuracy: different: 0.9172 > 0.9168
- Test accuracy: same: 0.9252 == 0.9252
??This says manual method has lower 'best C' and higher'test accuracy'in cross validation.
One of the possible reasons why this happens is that the way to calcualte 'average' is diffrent. In the manual method, it is 'the sum of accuracies over all nfolds per one of Cs that is used to comapre and find the best C is. On the other hand, the GridSearchCV uses 'the sum of accuracies over all Cs per one of n-folds'. ??Is this correct? If yes, why? If no, what makes the difference?
How does this model you've obtained perform on the test set?
The test results were the same accuracy, 0.9252.
As for 'how GridSearchCV performs', it implements a “fit” and a “score” method....??Is this what Q is asking?
fitmodel.best_estimator_, fitmodel.best_params_, fitmodel.best_score_, fitmodel.cv_results_
## Note¶
Manual CV
Manual method also has some attributes we can control as follows.
shuffle : bool, default=False Whether to shuffle the data before splitting into batches. Note that the samples within each split will not be shuffled. random_state : int, RandomState instance or None, default=None When `shuffle` is True, `random_state` affects the ordering of the indices, which controls the randomness of each fold. Otherwise, this parameter has no effect. Pass an int for reproducible output across multiple function calls. See :term:`Glossary <random_state>`.
- 3.2. Tuning the hyper-parameters of an estimator Hyper-parameters are parameters that are not directly learnt within estimators. In scikit-learn they are passed as arguments to the constructor of the estimator classes.
- GridSearchCV== exhaustively generates candidates from a grid of parameter values
-
‘accuracy’ == sklearn.metrics.accuracy_score
GraiSearch fnunction does not have a function of K-Fold. Is this correct? => No, it's not correct.
cv : int, cross-validation generator or an iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:- None, to use the default 5-fold cross validation,
- integer, to specify the number of folds in a
(Stratified)KFold, - :term:
CV splitter, An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs, if the estimator is a classifier and
yis either binary or multiclass, :class:StratifiedKFoldis used. In all other cases, :class:KFoldis used. These splitters are instantiated withshuffle=Falseso the splits will be the same across calls.Refer :ref:
User Guide <cross_validation>for the various cross-validation strategies that can be used here... versionchanged:: 0.22
cvdefault value if None changed from 3-fold to 5-fold.
#¶
A Walkthrough of the Math Behind Logistic Regression¶
Setting up Some Demo Code¶
Let's first set some code up for classification that we will need for further discussion on the math. We first set up a function cv_optimize which takes a classifier clf, a grid of hyperparameters (such as a complexity parameter or regularization parameter) implemented as a dictionary parameters, a training set (as a samples x features array) Xtrain, and a set of labels ytrain. The code takes the traning set, splits it into n_folds parts, sets up n_folds folds, and carries out a cross-validation by splitting the training set into a training and validation section for each fold for us. It prints the best value of the parameters, and retuens the best classifier to us.
def cv_optimize(clf, parameters, Xtrain, ytrain, n_folds=5):
gs = sklearn.model_selection.GridSearchCV(clf, param_grid=parameters, cv=n_folds)
gs.fit(Xtrain, ytrain)
print("BEST PARAMS", gs.best_params_)
best = gs.best_estimator_
return best
We then use this best classifier to fit the entire training set. This is done inside the do_classify function which takes a dataframe indf as input. It takes the columns in the list featurenames as the features used to train the classifier. The column targetname sets the target. The classification is done by setting those samples for which targetname has value target1val to the value 1, and all others to 0. We split the dataframe into 80% training and 20% testing by default, standardizing the dataset if desired. (Standardizing a data set involves scaling the data so that it has 0 mean and is described in units of its standard deviation. We then train the model on the training set using cross-validation. Having obtained the best classifier using cv_optimize, we retrain on the entire training set and calculate the training and testing accuracy, which we print. We return the split data and the trained classifier.
from sklearn.model_selection import train_test_split
def do_classify(clf, parameters, indf, featurenames, targetname, target1val, standardize=False, train_size=0.8):
subdf=indf[featurenames]
if standardize:
subdfstd=(subdf - subdf.mean())/subdf.std()
else:
subdfstd=subdf
X=subdfstd.values
y=(indf[targetname].values==target1val)*1
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, train_size=train_size)
clf = cv_optimize(clf, parameters, Xtrain, ytrain)
clf=clf.fit(Xtrain, ytrain)
training_accuracy = clf.score(Xtrain, ytrain)
test_accuracy = clf.score(Xtest, ytest)
print("Accuracy on training data: {:0.2f}".format(training_accuracy))
print("Accuracy on test data: {:0.2f}".format(test_accuracy))
return clf, Xtrain, ytrain, Xtest, ytest
Logistic Regression: The Math¶
dflog.head()
We could approach classification as linear regression, there the class, 0 or 1, is the target variable $y$. But this ignores the fact that our output $y$ is discrete valued, and futhermore, the $y$ predicted by linear regression will in general take on values less than 0 and greater than 1. Additionally, the residuals from the linear regression model will *not* be normally distributed. This violation means we should not use linear regression.
But what if we could change the form of our hypotheses $h(x)$ instead?
The idea behind logistic regression is very simple. We want to draw a line in feature space that divides the '1' samples from the '0' samples, just like in the diagram above. In other words, we wish to find the "regression" line which divides the samples. Now, a line has the form $w_1 x_1 + w_2 x_2 + w_0 = 0$ in 2-dimensions. On one side of this line we have
?? Is w a hyperparameter? =>This is coefficient. Not, hyper parameter.
$$w_1 x_1 + w_2 x_2 + w_0 \ge 0,$$and on the other side we have
$$w_1 x_1 + w_2 x_2 + w_0 < 0.$$Our classification rule then becomes:
\begin{eqnarray*} y = 1 &\mbox{ if}& \v{w}\cdot\v{x} \ge 0\\ y = 0 &\mbox{ if}& \v{w}\cdot\v{x} < 0 \end{eqnarray*}where $\v{x}$ is the vector $\{1,x_1, x_2,...,x_n\}$ where we have also generalized to more than 2 features.
?? Each vector represents each sample? => yes
?? For example, x1 can be person height, x2 is person weight? => yes
?? w is hyperparameter? => No
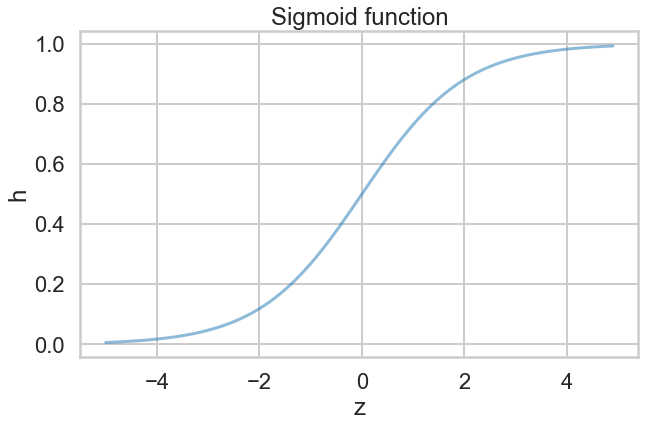
What hypotheses $h$ can we use to achieve this? One way to do so is to use the sigmoid function:
$$h(z) = \frac{1}{1 + e^{-z}}.$$Notice that at $z=0$ this function has the value 0.5. If $z > 0$, $h > 0.5$ and as $z \to \infty$, $h \to 1$. If $z < 0$, $h < 0.5$ and as $z \to -\infty$, $h \to 0$. As long as we identify any value of $y > 0.5$ as 1, and any $y < 0.5$ as 0, we can achieve what we wished above.
This function is plotted below:
h = lambda z: 1. / (1 + np.exp(-z))
zs=np.arange(-5, 5, 0.1)
fig, axes = plt.subplots(1, 1, figsize=(10,6))
axes.set_xlabel('z')
axes.set_ylabel('h')
axes.set_title('Sigmoid function')
plt.plot(zs, h(zs), alpha=0.5);
So we then come up with our rule by identifying:
$$z = \v{w}\cdot\v{x}.$$Then $h(\v{w}\cdot\v{x}) \ge 0.5$ if $\v{w}\cdot\v{x} \ge 0$ and $h(\v{w}\cdot\v{x}) \lt 0.5$ if $\v{w}\cdot\v{x} \lt 0$, and:
\begin{eqnarray*} y = 1 &\mbox{ if}& h(\v{w}\cdot\v{x}) \ge 0.5\\ y = 0 &\mbox{ if}& h(\v{w}\cdot\v{x}) \lt 0.5. \end{eqnarray*}We will show soon that this identification can be achieved by ?? minimizing a loss in the ERM framework called the log loss :
??Does this mean make it close to zero? or negative infinity?
=> Close to zero.
?? This looks like sum of
- (label) x (log of probability of the label)
- (the other label) x (log of probability of the other label)
but, what does this sum mean?
We will also add a regularization term:
where $C$ is Inverse of regularization strength (equivalent to $1/\alpha$ from the Ridge case), and smaller values of $C$ mean stronger regularization (punishment). As before, the regularization tries to prevent features from having terribly high weights (??), thus implementing a form of feature selection (??).
How did we come up with this loss? We'll come back to that, but let us see how logistic regression works out.
dflog.head()
clf_l, Xtrain_l, ytrain_l, Xtest_l, ytest_l = do_classify(LogisticRegression(),
{"C": [0.01, 0.1, 1, 10, 100]},
dflog, ['Weight', 'Height'], 'Gender','Male')
Xtrain_l
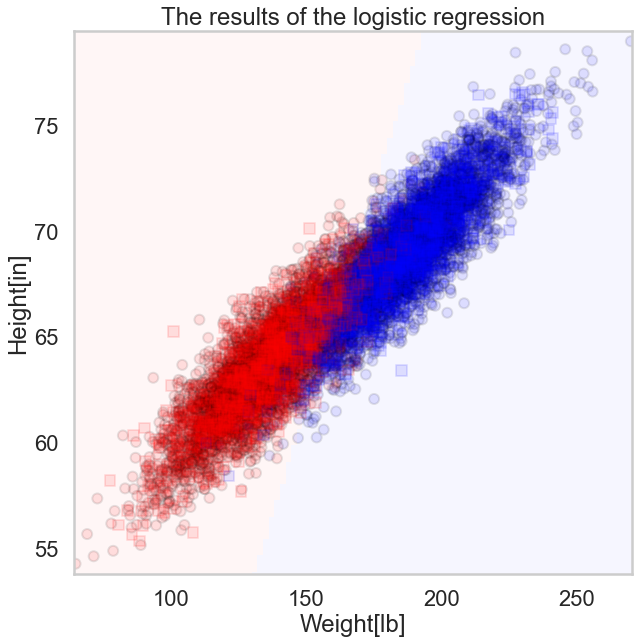
fig, axes = plt.subplots(1, 1, figsize=(10,10))
axes.set_xlabel('Weight[lb]')
axes.set_ylabel('Height[in]')
axes.set_title('The results of the logistic regression')
ax=plt.gca()
points_plot(ax, Xtrain_l, Xtest_l, ytrain_l, ytest_l, clf_l, alpha=0.1,psize=100);
# ??How can this figure size be changed?
In the figure here showing the results of the logistic regression, we plot the actual labels of both the training(circles) and test(squares) samples. The 0's (females) are plotted in red, the 1's (males) in blue. We also show the classification boundary, a line (to the resolution of a grid square). Every sample on the red background side of the line will be classified female, and every sample on the blue side, male. Notice that most of the samples are classified well, but there are misclassified people on both sides, as evidenced by leakage of dots or squares of one color onto the side of the other color. Both test and traing accuracy are about 92%.
The Probabilistic Interpretaion¶
Remember we said earlier that if $h > 0.5$ we ought to identify the sample with $y=1$? One way of thinking about this is to identify $h(\v{w}\cdot\v{x})$ with the probability that the sample is a '1' ($y=1$). Then we have the intuitive notion that lets identify a sample as 1 if we find that the probabilty of being a '1' is $\ge 0.5$.
So suppose we say then that the probability of $y=1$ for a given $\v{x}$ is given by $h(\v{w}\cdot\v{x})$?
Then, the conditional probabilities of $y=1$ or $y=0$ given a particular sample's features $\v{x}$ are:
\begin{eqnarray*} P(y=1 | \v{x}) &=& h(\v{w}\cdot\v{x}) \\ P(y=0 | \v{x}) &=& 1 - h(\v{w}\cdot\v{x}). \end{eqnarray*}?? These two can be written together as ?? What does y mean? ?? y of (A&B) or y of A ?
$$P(y|\v{x}, \v{w}) = h(\v{w}\cdot\v{x})^y \left(1 - h(\v{w}\cdot\v{x}) \right)^{(1-y)} $$?? Then multiplying over the samples, we get the probability of the training $y$ given $\v{w}$ and the $\v{x}$:
$$P(y|\v{x},\v{w}) = P(\{y_i\} | \{\v{x}_i\}, \v{w}) = \prod_{y_i \in \cal{D}} P(y_i|\v{x_i}, \v{w}) = \prod_{y_i \in \cal{D}} h(\v{w}\cdot\v{x_i})^{y_i} \left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}$$Why use probabilities? Earlier, we talked about how the regression function $f(x)$ never gives us the $y$ exactly, because of noise. This hold for classification too. Even with identical features, a different sample may be classified differently.
We said that another way to think about a noisy $y$ is to imagine that our data $\dat$ was generated from a joint probability distribution $P(x,y)$. Thus we need to model $y$ at a given $x$, written as $P(y|x)$, and since $P(x)$ is also a probability distribution, we have:
$$P(x,y) = P(y | x) P(x)$$and can obtain our joint probability $P(x, y)$.
Indeed its important to realize that a particular training set can be thought of as a draw from some "true" probability distribution (just as we did when showing the hairy variance diagram). If for example the probability of classifying a test sample as a '0' was 0.1, and it turns out that the test sample was a '0', it does not mean that this model was necessarily wrong. After all, in roughly a 10th of the draws, this new sample would be classified as a '0'! But, of-course its more unlikely than its likely, and having good probabilities means that we'll be likely right most of the time, which is what we want to achieve in classification. And furthermore, we can quantify this accuracy.
Thus its desirable to have probabilistic, or at the very least, ranked models of classification where you can tell which sample is more likely to be classified as a '1'. There are business reasons for this too. Consider the example of customer "churn": you are a cell-phone company and want to know, based on some of my purchasing habit and characteristic "features" if I am a likely defector. If so, you'll offer me an incentive not to defect. In this scenario, you might want to know which customers are most likely to defect, or even more precisely, which are most likely to respond to incentives. Based on these probabilities, you could then spend a finite marketing budget wisely.
Maximizing the Probability of the Training Set¶
Now if we maximize $P(y|\v{x},\v{w})$, we will maximize the chance that each point is classified correctly, which is what we want to do. While this is not exactly the same thing as maximizing the 1-0 training risk, it is a principled way of obtaining the highest probability classification. This process is called maximum likelihood estimation since we are maximising the likelihood of the training data y,
?? which is correct? y of x, or y of (x & w) => y given x
$$\like = P(y|\v{x},\v{w}).$$Maximum likelihood is one of the corenerstone methods in statistics, and is used to estimate probabilities of data.
We can equivalently maximize
$$\loglike = \log{P(y|\v{x},\v{w})}$$since the natural logarithm $\log$ is a monotonic function. This is known as maximizing the log-likelihood. Thus we can equivalently minimize a risk that is the negative of $\log(P(y|\v{x},\v{w}))$:
$$R_{\cal{D}}(h(x)) = -\loglike = -\log \like = -\log{P(y|\v{x},\v{w})}.$$Thus
\begin{eqnarray*} R_{\cal{D}}(h(x)) &=& -\log\left(\prod_{y_i \in \cal{D}} h(\v{w}\cdot\v{x_i})^{y_i} \left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}\right)\\ &=& -\sum_{y_i \in \cal{D}} \log\left(h(\v{w}\cdot\v{x_i})^{y_i} \left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}\right)\\ &=& -\sum_{y_i \in \cal{D}} \log\,h(\v{w}\cdot\v{x_i})^{y_i} + \log\,\left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}\\ &=& - \sum_{y_i \in \cal{D}} \left ( y_i \log(h(\v{w}\cdot\v{x})) + ( 1 - y_i) \log(1 - h(\v{w}\cdot\v{x})) \right ) \end{eqnarray*}This is exactly the risk we had above, leaving out the regularization term (which we shall return to later) and was the reason we chose it over the 1-0 risk.
Notice that this little process we carried out above tells us something very interesting: Probabilistic estimation using maximum likelihood is equivalent to Empiricial Risk Minimization using the negative log-likelihood, since all we did was to minimize the negative log-likelihood over the training samples.
sklearn will return the probabilities for our samples, or for that matter, for any input vector set $\{\v{x}_i\}$, i.e. $P(y_i | \v{x}_i, \v{w})$:
clf_l.predict_proba(Xtest_l)
Discriminative vs Generative Classifier¶
Logistic regression is what is known as a discriminative classifier as we learn a soft boundary between/among classes. Another paradigm is the generative classifier where we learn the distribution of each class. For more examples of generative classifiers, look here.
Let us plot the probabilities obtained from predict_proba, overlayed on the samples with their true labels:
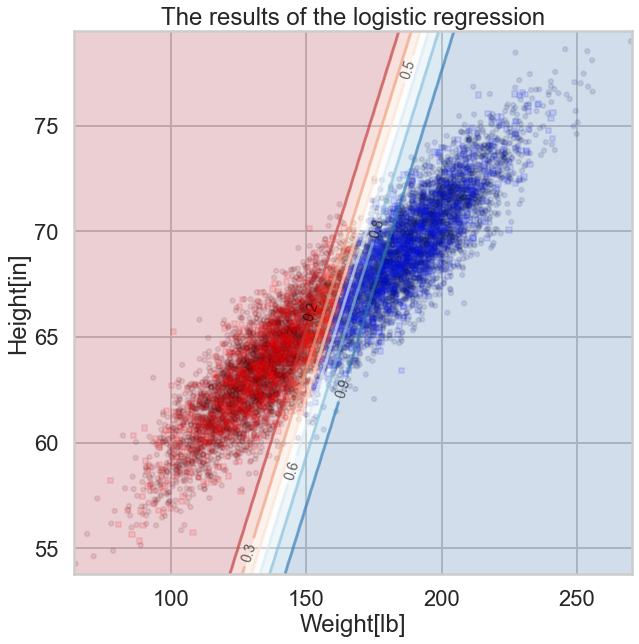
fig, axes = plt.subplots(1, 1, figsize=(10,10))
axes.set_xlabel('Weight[lb]')
axes.set_ylabel('Height[in]')
axes.set_title('The results of the logistic regression')
ax = plt.gca()
points_plot_prob(ax, Xtrain_l, Xtest_l, ytrain_l, ytest_l, clf_l, psize=20, alpha=0.1);
Notice that lines of equal probability, as might be expected are stright lines.(?? Why is this a straight line?) What the classifier does is very intuitive: if the probability is greater than 0.5, it classifies the sample as type '1' (male), otherwise it classifies the sample to be class '0'. Thus in the diagram above, where we have plotted predicted values rather than actual labels of samples, there is a clear demarcation at the 0.5 probability line.
Again, this notion of trying to obtain the line or boundary of demarcation is what is called a discriminative classifier. The algorithm tries to find a decision boundary that separates the males from the females. To classify a new sample as male or female, it checks on which side of the decision boundary the sample falls, and makes a prediction. In other words we are asking, given $\v{x}$, what is the probability of a given $y$, or, what is the likelihood $P(y|\v{x},\v{w})$?